When two lines intersect they form two pairs of opposite angles, A + C and B + D. Another word for opposite angles are vertical angles.

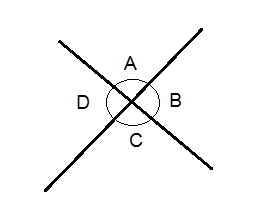
Vertical angles are always congruent, which means that they are equal.

Adjacent angles are angles that come out of the same vertex. Adjacent angles share a common ray and do not overlap.

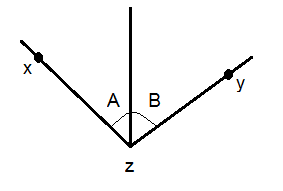
The size of the angle xzy in the picture above is the sum of the angles A and B.

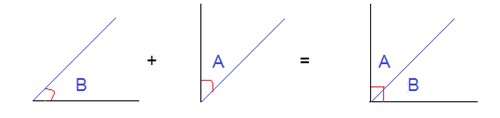
Two angles are said to be complementary when the sum of the two angles is 90°.

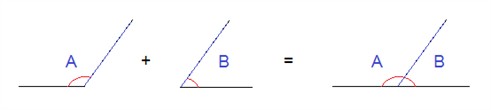
Two angles are said to be supplementary when the sum of the two angles is 180°.

If we have two parallel lines and have a third line that crosses them as in the ficture below – the crossing line is called a transversal

When a transversal intersects with two parallel lines eight angles are produced.

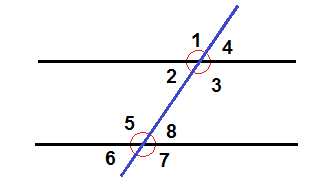
The eight angles will together form four pairs of corresponding angles. Angles 1 and 5 constitutes one of the pairs. Corresponding angles are congruent. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs e.g. 3 + 7, 4 + 8 and 2 + 6.

Angles that are in the area between the parallel lines like angle 2 and 8 above are called interior angles whereas the angles that are on the outside of the two parallel lines like 1 and 6 are called exterior angles.

Angles that are on the opposite sides of the transversal are called alternate angles e.g. 1 + 8.

All angles that are either exterior angles, interior angles, alternate angles or corresponding angles are all congruent.

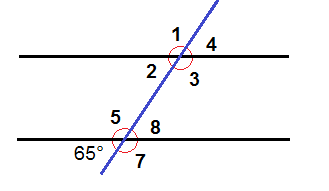
The picture above shows two parallel lines with a transversal. The angle 6 is 65°. Is there any other angle that also measures 65°?

6 and 8 are vertical angles and are thus congruent which means angle 8 is also 65°.

6 and 2 are corresponding angles and are thus congruent which means angle 2 is 65°.

6 and 4 are alternate exterior angles and thus congruent which means angle 4 is 65°.